本文最后更新于:2025年4月24日 下午
已知函数\(f(x)=a\ln x-\sinx+x\),其中\(a\)为非零常数.
(1)若函数\(f(x)\)在\((0,+\infty)\)上单调递增,求\(a\)的取值范围;
(2)设\(\theta\in(\pi,\dfrac{3}{2}\pi)\),且\(\cos\theta=1+\theta\sin\theta\),证明:当\(\theta^2\sin\theta<a<0\)时,函数\(f(x)\)在\((0,2\pi)\)上恰有两个极值点.
解析:(2)\(f'(x)=\dfrac{a}{x}-\cos x+1=\dfrac{a-x\cosx+x}{x}\)
设\(g(x)=x\cos{x}-x\),注意到\(g(0)=g(2\pi)=0\),并且\(g(\theta)=\theta\cos\theta-\theta=\theta^2\sin\theta\),该值恰好是条件\(\theta^2\sin\theta<a<0\)的端点值,为了使得\(g(x)=a\)有两个解,因此我们推测\(g(x)\)的图像应该如图所示:
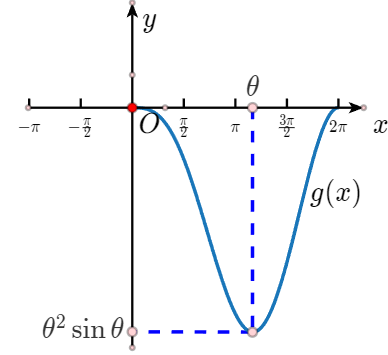
于是需要说明\(g(x)\)在\((0,\theta)\)单减,\((\theta,2\pi)\)单增,为此研究\(g'(x)=\cos x-x\sin x-1\),注意到\(g'(0)=g'(2\pi)=0\),\(g'(\theta)=\cos\theta-\theta\sin\theta-1=0\),因此我们推测\(g'(x)\)的图象应该如图所示:
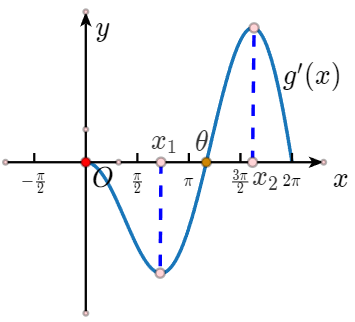
于是需要说明\(x\in(0,\theta)\)时,\(g'(x)<0\),\(x\in(\theta,2\pi)\)时,\(g'(x)>0\).但是我们只能方便证明\(x\in(0,\pi)\)时,\(g'(x)=\cos x-1-x\sinx<0\),为了证明其它区间\(g'(x)\)的符号,需要结合\(g'(x)\)的单调性,也就是要说明\(g'(x)\)在\((0,x_1)\)单减,\((x_1,x_2)\)单增,\((x_2,2\pi)\)单减,为此研究\(g''(x)=-2\sin x-x\cosx\),注意到\(g''(0)=0,g''(\dfrac{3\pi}{2})=2,g''(2\pi)=-2\pi\),因此我们推测\(g''(x)\)的图象应该如图所示:
当\(x\in(\pi,\dfrac{3\pi}{2})\)时,\(g''(x)=-2\sin x-x\cosx>0\),于是\(g'(x)\)在\((\pi,\dfrac{3\pi}{2})\)单增,由于\(g'(\theta)=0\),那么\(x\in(\pi,\theta)\)时,\(g'(\theta)<0\),\(x\in(\theta,\dfrac{3\pi}{2})\)时,\(g'(\theta)>0\),至此\(x\in(0,\theta)\)时,\(g'(x)<0\)说明完毕,接下来只需要证明\(x\in(\dfrac{3\pi}{2},2\pi)\)时,\(g'(x)>0\)即可,只需要说明\(g'(x)\)在\((\dfrac{3\pi}{2},x_2)\)单增,亦即\(g''(x)>0\), \(g'(x)\)在\((x_2,2\pi)\)单减,亦即\(g''(x)<0\),于是需要借助\(g''(x)\)的单调性,再次求导\(g'''(x)=-3\cos x+x\sinx\),惊喜发现\(x\in(\dfrac{3\pi}{2},2\pi)\)时,\(g'''(x)<0\),因此\(g''(x)\)在\(x\in(\dfrac{3\pi}{2},2\pi)\)单减,由于\(g''(\dfrac{3\pi}{2})=2,g''(2\pi)=-2\pi\),于是\(\existsx_2\in(\dfrac{3\pi}{2},2\pi)\)使得\(g''(x_2)=0\),至此思路全部打通。
最终正常顺序简述为:
本题以单调性为主线(红色部分),采取分段证明的策略,每次求导都能容易看到在部分区间上导数的符号(绿色部分),然后结合特殊点处的函数值(黄色部分),判断各导函数是否存在零点,从而决定上级导函数的单调性。

