2021新高考1卷部分试题解析

2021新高考全国1卷

8.有6个相同的球，分别标有数字1，2，3，4，5，6，从中有放回的随机取两次，每次取1个球.甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则（ ）

\(A.\)甲与丙相互独立 \(B.\)甲与丁相互独立 \(C.\)乙与丙相互独立 \(D.\)丙与丁相互独立

解：甲与丙是互斥事件，故不相互独立；\(P\)(丁|甲)=\(P\)(丁)=\(\dfrac{1}{6}\)，故甲与丁相互独立

\(P\)(丙)=\(\dfrac{5}{36}\)，\(P\)(丙|乙)=\(\dfrac{1}{6}\)，故乙与丙不相互独立；丙与丁是互斥事件，故丙与丁不相互独立

12.在正三棱柱\(ABC-A_1B_1C_1\)中，\(AB=AA_1=1\)，点\(P\)满足\(\overrightarrow{BP}=\lambda\overrightarrow{BC}+\mu\overrightarrow{BB_1}\)，其中\(\lambda\in[0,1],\mu\in[0,1]\)，则（ ）

\(A.\)当\(\lambda=1\)时，\(\triangle AB_1P\)的周长为定值

\(B.\)当\(\mu=1\)时，三棱锥\(P-A_1BC\)的体积为定值

\(C.\)当\(\lambda=\dfrac{1}{2}\)时，有且仅有一个点\(P\)，使得\(A_1P\bot BP\)

\(D.\)当\(\mu=\dfrac{1}{2}\)时，有且仅有一个点\(P\)，使得$A_1B\(平面\)AB_1P$

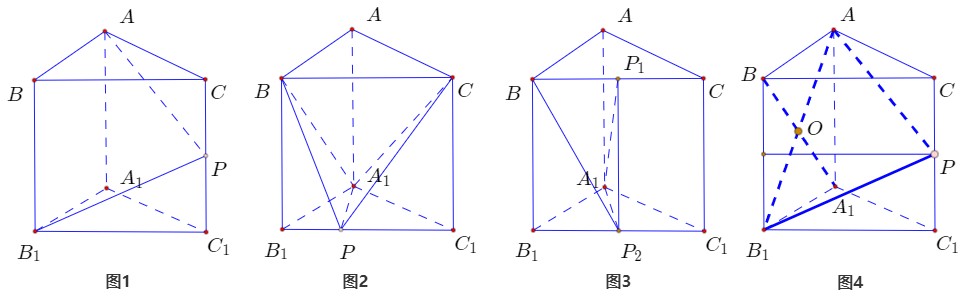
解：对于\(A\)，点\(P\)在线段\(CC_1\)上，当\(P\)位于\(CC_1\)的中点时，\(AP+B_1P\)最短，故\(\triangle AB_1P\)的周长不是定值，\(A\)错

对于\(B\)，点\(P\)在线段\(B_1C_1\)上，由于\(B_1C_1//\)平面\(A_1BC\)，则\(B_1C_1\)上任意一点到平面的距离都相等，故\(B\)对

对于\(C\)，点\(P\)在线段\(P_1P_2\)上，当\(P\)在\(P_1\)或\(P_2\)上时，都有\(A_1P\bot BP\)，\(C\)错，多选题故\(D\)正确

对于\(D\)，需满足\(A_1B\bot PO\)，由于\(O\)为\(A_1B\)的中点，即需有\(PB=PA_1\)，则\(P\)在线段\(A_1B\)的中垂面上，而中垂面与\(P\)所在的线段交点唯一，即\(CC_1\)的中点

16.某校学生在研究民间剪纸艺术时，发现剪纸时经常会沿纸的某条对称轴把纸对折，规格为20dm \(\times\) 12dm的长方形纸，对折1次共可以得到10dm \(\times\) 12dm，20dm \(\times\) 6dm两种规格的图形，它们的面积之和为 \(S_1=240dm^2\)，对折2次共可以得到5dm \(\times\) 12dm，10dm \(\times\) 6dm，20dm \(\times\) 3dm三种规格的图形，它们的面积之和\(S_2=180dm^2\)，以此类推，则对折4次共可以得到不同规格图形的种数为_________； 如果对折\(n\)次，那么\(\sum _{k=1}^n S_k=\) ____________\(dm^2\)

解：考察数列错位相减法求和略，5，\(720-240\cdot\dfrac{n+3}{2^n}\)

19.记\(\triangle ABC\)的内角\(A,B,C\)的对边分别为\(a,b,c\).已知\(b^2=ac\)，点\(D\)在边\(AC\)上，\(BD\sin\angle ABC=a\sin C\).

（1）证明：\(BD=b\)；

（2）若\(AD=2DC\)，求\(\cos\angle ABC\).

解：（2）由\(\cos\angle ADB+\cos\angle CDB=0\)，即\(\dfrac{\dfrac{4}{9}b^2+b^2-c^2}{2\times\dfrac{2}{3}b^2}+\dfrac{b^2+\dfrac{1}{9}b^2-a^2}{2\times\dfrac{1}{3}b^2}=0\)，

化简得\(3c^2-11ac+6a^2=0\)，即\(c=3a\)或\(c=\dfrac{2}{3}a\)

若\(c=3a\)，则\(b=\sqrt3a\)，此时\(a+b<c\)，不能构成三角i形，舍

故\(c=\dfrac{2}{3}a\)，此时\(\cos \angle ABC=\dfrac{a^2+c^2-ac}{2ac}=\dfrac{7}{12}\)

21.在平面直角坐标系\(xOy\)中，已知点\(F_1(-\sqrt{17},0),F_2(\sqrt{17},0)\)，点\(M\)满足\(|MF_1|-|MF_2|=2\).记\(M\)的轨迹为\(C\).

（1）求\(C\)的方程

（2）设点\(T\)在直线\(x=\dfrac{1}{2}\)上，过\(T\)的两条直线分别交\(C\)于\(A,B\)两点和\(P,Q\)两点，且\(|TA|\cdot|TB|=|TP|\cdot|TQ|\)，求直线\(AB\)的斜率与直线\(PQ\)的斜率之和.

解：（1）\(C:x^2-\dfrac{y^2}{16}=1(x\ge1)\)

（2）方法一：设\(T(\dfrac{1}{2},n)\)，\(AB:y=k_1x+m_1\)，\(PQ:y=k_2x+m_2\)，将\(AB\)与\(C\)联立得

\((16-k_1^2)x^2-2k_1m_1x-m_1^2-16=0\)，设方程的两根为\(x_1,x_2\)

则\((16-k_1^2)x^2-2k_1m_1x-m_1^2-16=(16-k_1^2)(x-x_1)(x-x_2)\)，令\(x=\dfrac{1}{2}\)得

\((\dfrac{1}{2}-x_1)(\dfrac{1}{2}-x_2)=\dfrac{\dfrac{1}{4}(16-k_1^2)-k_1m-m_1^2-16}{16-k_1^2}=\dfrac{-12-(\dfrac{1}{2}k_1+m_1)^2}{16-k_1^2}=\dfrac{n^2+12}{k_1^2-16}\)

于是\(|TA|\cdot|TB|=(1+k_1^2)\dfrac{n^2+12}{k_1^2-16}\)，同理\(|TP|\cdot|TQ|=(1+k_2^2)\dfrac{n^2+12}{k_2^2-16}\)

故\(\dfrac{1+k_1^2}{k_1^2-16}=\dfrac{1+k_2^2}{k_2^2-16}\)，即\(1+\dfrac{17}{k_1^2-16}=1+\dfrac{17}{k_2^2-16}\)，

故\(k_1^2=k_2^2\)，由于\(k_1\ne k_2\)，则\(k_1=-k_2\)，即\(k_1+k_2=0\)

方法二：设\(T(\dfrac{1}{2},n)\)，直线\(AB\)的参数方程为\(\begin{cases} x=\dfrac{1}{2}+t\cos\alpha\ \\ y=n+t\sin\alpha \end{cases},t\)为参数，与\(C\)联立得

\((16\cos^2\alpha-\sin^2\alpha)t^2+(16\cos\alpha-2n\sin\alpha)t-12-n^2=0\)

于是\(|TA|\cdot|TB|=t_1t_2=\dfrac{-n^2-12}{16\cos^2\alpha-\sin^2\alpha}=\dfrac{-n^2-12}{17\cos^2\alpha-1}\)

设直线\(PQ\)的参数方程为\(\begin{cases} x=\dfrac{1}{2}+t\cos\beta\ \\ y=n+t\sin\beta \end{cases},t\)为参数

同理\(|TP|\cdot|TQ|=\dfrac{-n^2-12}{16\cos^2\beta-\sin^2\beta}=\dfrac{-n^2-12}{17\cos^2\beta-1}\)

于是\(\cos^2\alpha=\cos^2\beta\)，由于\(\alpha\ne\beta\)，则\(\alpha+\beta=\pi\)，即\(AB\)与\(PQ\)的斜率之和为0

老教材《坐标系与参数方程》选修教材的例题（原例题是椭圆），出现在新高考挺尬的

22.已知函数\(f(x)=x(1-\ln x)\)

（1）讨论\(f(x)\)的单调性；

（2）设\(a,b\)为两个不相等的正数，且\(b\ln a-a\ln b=a-b\)，证明：\(2<\dfrac{1}{a}+\dfrac{1}{b}<e\)

解：（1）\(f'(x)=-\ln x\)，则\(f(x)\)在\((0,1)\)单增，\((1,+\infty)\)单减

（2）\(b\ln a-a\ln b=a-b\)即\(\dfrac{1}{a}(1-\ln\dfrac{1}{a})=\dfrac{1}{b}(1-\ln\dfrac{1}{b})\)，令\(x_1=\dfrac{1}{a},x_2=\dfrac{1}{b}\)

即\(f(x_1)=f(x_2)\)，\(x_1\ne x_2\)，证明：\(2<x_1+x_2<e\)

左侧证明为标准的极值点偏移问题，略，下证明右边

方法一：仿照极值点偏移的求解，统一变量构造函数

易知\(0<x_1<1<x_2<e\)，只需证\(x_2<e-x_1\)，只需证\(f(x_2)>f(e-x_1)\)，即证\(f(x_1)>f(e-x_1)\)

令\(g(x)=f(x)-f(e-x)=x(1-\ln x)-(e-x)(1-\ln(e-x))=2x-x\ln x+(e-x)\ln(e-x)-e,x\in(0,1)\)

则\(g'(x)=-\ln(ex-x^2)\)，记\(x_0\)为\(ex-x^2=1\)的小于1的根，则\(g(x)\)在\((0,x_0)\)单增，\((x_0,\dfrac{e}{2})\)单减

又\(x\rightarrow 0\)时，\(g(x)\rightarrow 0\)，结合\(g(x)>g(\dfrac{e}{2})=0\)知，\(g(x)>0,x\in(0,1)\)成立

如果想避免上述极限的写法，考虑对\(g(x)\)的解析式进行变形，令\(h(x)=2-\ln x+\dfrac{e-x}{x}\ln(e-x)-\dfrac{e}{x}\)

\(h'(x)=-\dfrac{1}{x^2}[e\ln(e-x)+2x-e]\)，令\(\varphi(x)=e\ln(e-x)+2x-e\)，注意\(\varphi(0)=0\)

\(\varphi'(x)=\dfrac{2x-e}{x-e}\)，当\(x\in(0,\dfrac{e}{2})\)时，\(\varphi'(x)>0\)，则\(\varphi(x)>0\)，即\(h'(x)<0\)，故\(h(x)\)在\((0,\dfrac{e}{2})\)单减，则\(h(x)>h(\dfrac{e}{2})=0\)

方法二：比值换元，统一变量

令\(x_2=tx_1\)，即有\(\begin{cases}x_1(1-\ln x_1)=x_2(1-\ln x_2)\\ x_2=tx_1 \end{cases}\)，解得\(\ln x_1=1-\dfrac{t\ln t}{t-1}\)

\(x_1+x_2<e\)，即证\((1+t)x_1<e\)，即证\(\ln(1+t)+\ln x_1<1\)，即证\(\ln(1+t)-\dfrac{t\ln t}{t-1}<0\)，即证\(\dfrac{\ln(t+1)}{t}<\dfrac{\ln t}{t-1}\)，

令\(g(t)=\dfrac{\ln t}{t-1}(t>1)\)，则\(g'(t)=\dfrac{t-1-t\ln t}{t(t-1)}<0\)，于是\(g(t)\)在\((1,+\infty)\)单减，则\(g(t+1)<g(t)\)，得证

方法三：切线放缩

\(f(x)\)在\(x=e\)处的切线方程为\(y=-x+e\)，

令\(g(x)=x(1-\ln x)+x-e=2x-x\ln x-e\)，\(g'(x)=1-\ln x\)，于是\(g(x)\)在\((0,e)\)单增，\((e,+\infty)\)单减，即\(g(x)\le g(e)=0\)

设\(x_1(1-\ln x_1)=x_2(1-\ln x_2)=-x_2'+e\)，由于\(x_2(1-\ln x_2)<-x_2+e\)，则\(x_2<x_2'\)

于是\(x_1+x_2<x_1+x_2'=x_1+[e-x_1(1-\ln x_1)]=e+x_1\ln x_1<e\)成立

方法四：割线放缩

\(f(x)\)经过\((0,0)\)和\((1,1)\)两点的割线方程为\(y=x\)

显然当\(x\in(0,1)\)时，\(x(1-\ln x)>x\)

设\(x_1(1-\ln x_1)=x_1'=x_2(1-\ln x_2)\)，由于\(x_1(1-\ln x_1)>x_1\)，则\(x_1'>x_1\)

于是\(x_1+x_2<x_1'+x_2=x_2(1-\ln x_2)+x_2=2x_2-x_2\ln x_2\)

令\(g(x)=2x-x\ln x,x\in(1,e)\)，则\(g'(x)=1-\ln x\)，于是\(g(x)\)在\((1,e)\)单增

则\(g(x)<g(e)=e\)，即\(2x_2-x_2\ln x_2<e\)，得证

将法二和法三综合起来，切割线一起放缩：\(x_1+x_2<x_1'+x_2'=e\)

事实上相当于用对称轴为\(x=\dfrac{e}{2}\)的函数\(y=\dfrac{e}{2}-|x-\dfrac{e}{2}|\)拟合了\(f(x)\)，体现化曲为直的思想

娱乐一下：当然也可以考虑用对称轴为\(x=\dfrac{e}{2}\)的二次函数拟合，利用待定系数得\(y=\dfrac{1}{1-e}(x-\dfrac{e}{2})^2+\dfrac{e^2}{4(e-1)}\)

方法五：野猪wj

\(b\ln a-a\ln b=a-b\)即\(\dfrac{1}{a}(1+\ln a)=\dfrac{1}{b}（1+\ln b)\)，即\(\dfrac{1}{a}\ln ea=\dfrac{1}{b}\ln eb\)，即\(\dfrac{1}{ea}\ln \dfrac{1}{ea}=\dfrac{1}{eb}\ln \dfrac{1}{eb}\)

令\(\dfrac{1}{ea}=x_1,\dfrac{1}{eb}=x_2\)，\(g(x)=x\ln x\)，即\(g(x_1)=g(x_2)\)，证明：\(\dfrac{2}{e}<x_1+x_2<1\)

这样同构的式子变化，使得函数解析式变得更加漂亮，下面证明类似略